為了討論直升機的動力學問題，先對直升機的類別進行簡介。按照旋翼的數目與配置以及葉片數目來區分，直升機有如下幾種：

單旋翼直升機

顧名思義，單旋翼直升機就是它只有一個旋翼。一般它必須帶一個尾槳負責抵消旋翼產生的反轉矩。例如，歐洲直升機公司制造的EC-135直升機。

圖1就是一個帶尾槳的單旋翼直升機圖片。

但是，也有單旋翼直升機無尾槳的情況，這時它的機身尾部側面有空氣排出管道，用噴氣的反作用力來抵消旋翼產生的反轉矩。例如，美國麥道直升機公司生產的MD520N直升機。“旋翼產生的反轉矩”將是本文的討論的重點。

雙旋翼直升機

雙旋翼直升機具有兩個旋翼。兩個旋翼的排列有如下三個情況：

縱列式：兩個旋翼前后縱向排列，旋轉方向相反。例如，美國波音公司制造的CH-47“支努干”運輸直升機。 ?

橫列式：兩個旋翼左右橫向排列，旋翼軸間隔較遠，旋轉方向相反。比如，前蘇聯的Mi-12直升機。

共軸式：兩個旋翼上下排列，在同一個轉軸線上，互成反向旋轉。例如，前蘇聯的卡-50武裝直升機。（請見圖7的共軸式雙旋翼直升機圖片）

四旋翼直升機

圖2是中國研制的四旋翼無人直升機。四個旋翼分為兩對，分別以正螺旋和反螺旋方向旋轉。

葉片數量

葉片數量往往與載重量大小相關，常見有2，3，4，8 個葉片。例如米-8直升機有4個葉片；米-28有5個葉片；米-26直升機的旋翼有8個葉片，尾槳有5個葉片。2008年5月26日，一架紅色米-26直升機吊裝了一臺重約13.2噸的重型挖掘機，前往唐家山堰塞湖壩體。圖3為執行該項任務的米-26直升機照片。

圖3丨 “米-26”直升機

傾轉式旋翼飛機

美國V-22魚鷹直升機就是傾轉式旋翼飛機（參見圖4），它兼有直升機和飛機的共同優點。當旋翼的轉軸豎直時，旋翼產生升力。當轉軸角（與豎直軸的夾角）接近90度時，旋翼就變成螺旋槳，飛行速度由300公里/時，提高到500公里/時。現在，美國V-22部署到東亞美軍駐日基地，對中國進行威懾。

圖4丨V-22“魚鷹”傾斜（傾轉）式旋翼飛機

直升機旋翼動力學奧妙與動量矩守恒律

前邊提到，單旋翼直升機除了有一個大的旋翼外，在尾部還有一個小的尾旋翼（也叫尾槳）。圖5是一個帶鑲嵌式尾旋翼（尾槳）的直升機。尾槳產生的作用力沿水平方向，并且與機身垂直，對機身重心有一個力矩（轉矩）。再仔細看，尾槳力矩使機身轉動的方向必然和主旋翼的轉動方向相反。在設計時，要保證尾槳的轉矩與旋翼的動量矩大小相等方向相反。這樣直升機才能正常飛行。下面我們從力學原理出發來討論一下直升機運行的奧秘。

圖5丨帶鑲嵌式尾槳的直升機

動量矩定理 (Theorem of moment of momentum) 和動量矩守恒定律 (Law of conservation of moment of momentum) 是剛體（或質點系）運動必須滿足的動力學原理。動量矩定理說，動量矩對時間的變化率等于外加力矩之總和。當質點系不受外力作用或所受全部外力對某定點或定軸的主矩始終等于零時，該質點系對該點或該軸的動量矩保持不變。即當作用于它的外力矩之和為零時，它的動量矩變化率將等于零。這就是動量矩守恒定律。

為了更嚴格地說明動量矩定理和動量矩守恒定律，請看下邊的公式：

動量矩

質點對某點的動量矩為L0(mv)= rmv； 其中，黑體符號L0、 r、v都是向量。這個公式表明，質點m對0點的動量矩L0等于質點m到0點的矢徑r與其動量mv的矢量積。

剛體的動量矩為Lz=Jzω； 其中，Jz為剛體對于轉軸的轉動慣量，ω是角速度向量。

動量矩定理

動量矩對時間的變化率等于外加力矩之總和，就是：?

[Lz]' =∑Mz(Fi )

其中，等號左邊是對動量矩Lz求時間導數，右邊是對外力矩求和。

動量矩守恒定律

當上式的右端項為零時，Lz為常數，即動量矩永恒不變。直升機在空中飛行時，它的旋翼不停地旋轉，這將產生對直升機重心的動量矩。由于它是孤立系統，外界對它的外力矩之和為零，如果沒有尾槳的話，機身將不停地向旋翼旋轉的反向旋轉，這樣就難以執行所指定的各類任務。安裝尾槳就是要以尾槳的力矩平衡這個“旋翼產生的反轉矩”。這就是直升機安裝尾槳的力學意義。

為使機身不產生旋轉，也不安裝尾槳。聰明的工程師們設計了共軸式雙旋翼直升機（參見圖6）。它的兩幅旋翼安裝在同一個軸上，分別朝不同方向旋轉，二者的動量矩必須大小相等，構成平衡。若是雙軸兩旋翼情況（如V-22魚鷹直升機），要求兩個旋翼的轉動方向相反且動量矩相等。對于四軸四旋翼情況，很容易推斷，它們要兩兩成對，分別朝反向轉動，動量矩大小要相等，以保證總動量矩為零。

圖6丨共軸式雙旋翼直升機

剛體的轉動慣量

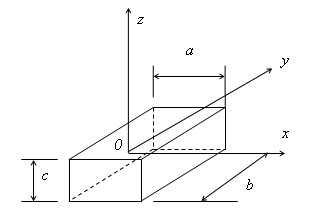
上節提到Jz為剛體對轉軸的轉動慣量，它和物體平動的慣性量（即質量）類似。當轉動慣量越大時，轉動它越困難，或者使它轉動角速度增大越困難。具有相同質量的物體，形狀不同，其轉動慣量大小不同。以圖7所示實心長方體為例。這是一個三維尺寸為aⅹbⅹc的長方體，為簡單起見，令b=2a=4c；根據理論力學教科書，有如下公式：

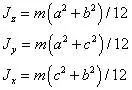
其中：Jz，Jy，Jx分別是繞z，y，x三個軸、對物體重心點0的轉動慣量。可見，Jz最大，Jx次之，Jy最小。

剛體的轉動慣量問題，和我們身邊的許多活動息息相關，這里以競技運動為例。體操和跳水運動員在做空翻或翻騰動作時，其身體的姿勢（形態）決定了其動作的難度，裁判打分時給不同的難度系數。例如圖8a 所示的跳水女運動員所做的團身空翻（或向后翻騰），她的身體曲折成三段，各部分身體重量最靠近于重心。于是，其轉動慣量最小，可以使翻騰速度最快。所以，在10米臺跳水做翻騰三周半的動作時都多采用團身翻騰。圖8b所示的則是曲體空翻（或向后翻騰），她的身體呈曲兩段折疊，其轉動慣量比團身情況稍大。難度系也較大。最難做的是圖8c所示的體操運動員所做的直體空翻。由于直體的轉動慣量最大，空翻最費力；難度系數最大。同時由于姿態優美，打分較高。

圖8a丨團身空翻

圖8b(左) 丨曲體空翻 ??? ? ?圖8c(右)丨 直體空翻

另外，與轉動慣量有關的例子還有高空走鋼絲。圖9是阿迪力在新疆喀納斯高空走鋼絲的照片。你看他兩手緊握一根很長的平衡桿。這根平衡桿與他的身體緊緊結合為一體，總的轉動慣量大大增加。一個很大轉動慣量的物體，是不易被轉動的，所以他的直立狀態較為穩定，比較安全。相反，如果沒有這個平衡桿，他煢煢一身走在鋼絲上，就很易翻倒。這就是走鋼絲的人必須握有平衡桿的力學奧秘。

圖9丨阿迪力新疆喀納斯高空走鋼絲

最后，和動量矩守恒有關的例子是陀螺儀，它是具有高速旋轉剛體轉子、服從動量矩守恒律的一種常用儀表。現代高精度的單自由度陀螺常是液浮、磁浮和氣浮并用的三浮陀螺儀。這種陀螺儀的精度極高。陀螺儀廣泛應用于各種運載體（如船舶、飛機等）上，成為各種運載體的自動控制、制導和導航系統中測定姿態、方位的重要元件。

華越無人機教育是廣東省首家無人機教育培訓機構，是華南區無人機駕駛證考試中心，無人機教員培訓中心，是廣東省規模最大、課程設置最完整的無人機培訓學校。同時也是直升機黃埔軍校，80%的直升機飛手都畢業于華越無人機教育。

最新開班信息： ? ?

3月 1 日 脫產53班開班

3月15日 脫產54班開班

3月4日無人機飛控知識技術講座

掃一掃，關注我們 ↓